The A+B Theorem

The Central Tenet of Douglas Social Credit

Last week, in The Forgotten Prophet, I began a review of the economic thought of Major C. H. Douglas, creator of social credit theory. This week’s essay continues where that one left off.

Some Caveats on Endorsement, Exploration, and Criticism

Before we proceed into the main body of the article, I want to offer three caveats. Feel free to skip these if you’re a busy Type A personality who doesn’t have time for such nonsense.

First, I do not mean for my exploration of Douglas’s thought to necessarily imply endorsement of it or of his solution in part or full. I explore a lot of thinkers, including the likes of Marx and Herbert Marcuse. But I certainly do not endorse all of their thoughts. Whenever I’m exploring a thinker, I attempt to do so from their point of view, seeing the world as they see it. This has, from time to time, led to some amusing accusations leveled against me by those who cannot conceive of temporarily taking on another person’s point of view without fully accepting that point of view.

Second, I cannot and do not claim to now be an expert on Douglas’s thought; in fact, the exercise of writing these essays is largely an exercise in seeing how well I understand it at all, as well as an opportunity to acquire fresh insights from those with other knowledge. You will do me no discourtesy to share your own thoughts on him, and to point out any errors in interpretation I have made.

However…

When presenting the ideas of thinkers in blog format, it is never possible to present what are often multi-book thoughts in full. As such, the ideas are left highly vulnerable to what I call “first-order criticism.” Let me give an example from a different field:

• Ufologist: “The US military is encountering UFOs regularly.”

• Skeptic: “If there were really that many UFOs, we would have photographic evidence of them. There’s billions of cameras on the planet.”

The skeptic has delivered the first-order criticism, and if the conversation ends there, he seems to have delivered a kill-shot. But the Ufologist has a second-order response (“given that we already have stealth aircraft and invisibility suits, it seems likely that technology capable of creating advanced aircraft can create means of avoiding photographic detection”). The skeptic might then have a second-order criticism, the ufologist a third-order response, and so on. Provided both proceed in good faith, then this manner of exchange can help interlocutors get at truth. Good books written about controversial ideas tend to be quite long because the writers will bring up the best arguments presented against their ideas and address them in this manner.

But both sides don’t usually proceed in good faith. A common tactic used by the fake media is to set up a controversial idea, present the first-order criticism of the idea by an orthodox expert in the field, and stop there. In this manner, the media can portray itself as having given a fair treatment to the idea while simultaneously guaranteeing that the reader is left believing the idea has been “debunked.” The same is true of online discourse — approximately 99.82% of all X comments are first-order criticisms. It’s rhetorically powerful.¹

But there’s little point in exploring controversial thinkers if one enters into the exploration with the goal of delivering rhetorical kill shots from our arsenal of accepted ideas rather than doing the hard cognitive work of thinking the new ideas through in full.

Hence my third caveat: If you are tempted to fire repeated first-order criticisms at Douglas’s thought, I’d ask that instead you query how Douglas answered the criticism, rather than assume he didn’t even see it. Now, on to the article…

In exploring Major Douglas’s thought, I have discovered that there is no one book that adequately summarizes it. His ideas are spread through a number of volumes, written over a span of about 20 years…. and seeds planted in 1919 sometimes do not bear fruit until 1930. Then, following Douglas, a number of other economists elaborated on his ideas in yet more fruitful ways. The effort of synthesizing this into a single comprehensive book would be Herculean.

Fortunately, such an effort has already been made, and the Herculean book exists. It is called Social Credit Economics, by M. Oliver Heydorn. Unlike Douglas’s work, Dr. Heydorn’s work is not available for free at the C. H. Douglas Institute, but you can purchase it at Amazon at the link. This book has become my tour guide through Douglas’s theories and I’ll be referencing it, along with Douglas’s own thought.

Introducing the A + B Theorem

The A + B theorem is of central importance to Douglas Social Credit. Heydorn explains the origin of the A+ B theorem as follows:

In 1916, Douglas was hired to sort out an accounting muddle at the Royal Aircraft Factory in Farnborough, England. This required him to examine the operation’s books carefully and to analyze, with the help of tabulating machines, the costs of aircraft production at the factory. On one fateful day.. Douglas realized that the total amount paid out by the factor in wages and salaries during any given week always feel short of the monetary value of the goods that it had produced that same week. There was a time lag between prices and incomes, i.e. the rate at which prices were being generated. As he himself noted, such an observation might have seemed (and might still seem) like a blunt statement of an obvious fact… But if this was true, then it was likely to be true every week and of every factory in the economy over the same period of time. The implications were staggering.

Douglas went on to study the books of over one hundred other British firms and was able to confirm that what was true of the Farnborough factory was indeed true of these other businesses as well: the amount of money paid out by them during any period of time was never sufficient, as a form of purchasing power in the hands of consumers, to purchase the goods and service that these same firms were producing during that same period.

By inferences from these observations, Douglas discovered the Social Credit theorem, more commonly known as the A + B Theorem from the proof that Douglas offered of it.

Douglas presented that proof in 1930 to the British Macmillan Committee on Finance and Industry. To the assembled ministers and economists (among them J. Maynard Keynes), he said:

A factory or other productive organization has besides its economic function as a producer of goods, a financial aspect — it may be regarded on the one hand as a device for the distribution of purchasing power to individuals, through the media of wages, salaries, and dividends; and on the hand as a manufactory of prices — financial values. From this standpoint its payments may be divided into two groups.

• Group A — All payments made to individuals (wages, salaries, and dividends)

• Group B — All payments to other organizations (raw materials, bank charges, and other external costs.)

Now the rate of flow of purchasing power to individuals is represented by A, but since all payments go into prices, the rate of flow of prices cannot be less than A plus A. Since A will not purchase A plus B, a proportion of the product of at least equivalent to B must be distributed by a form of purchasing power which is not comprised in the described grouped under A.

Douglas considered the A + B theorem to be “the vital theorem on which turns the immediate theory of civilization” and it is to address the problem posed by the theorem that Douglas introduced the notion of social credit. If the theorem is correct, something like social credit is necessary because industrial capitalism is fundamentally broken. Say’s Law does not hold; industrial production does not create sufficient demand to purchase its own supply.

Assessing the A + B Theorem

So… is the A + B theorem correct? Long-term readers of this blog will know that I largely subscribe to Austrian economics, specifically as presented by Professor George Reisman ins his book Capitalism (available for free from the Mises Institute). I’ve personally written about how Reisman’s circle flow of money solves the profit puzzle. Therefore I have entered into my study of Douglas’s work predisposed to reject it.

Douglas could, of course, assert that — whatever the merits or flaws of Austrian economic proofs — the Social Credit theorem is empirically correct based on Douglas’s own careful study of industry. As Heydorn explains:

In contradistinction to those economists who first devise a theory to explain economic behaviour and then employ statistical and econometric models in an attempt to reconcile the facts with the theory, it should be noted that Douglas first ascertained the facts of the situation before endeavoring to offer at theoretical account of them; he observed the methodological principle which insists on the priority of the given. The theorem is not to be interpreted, therefore, as something which preceded an empirical discovery of the relevant facts, but as an attempt to give an account of the actual facts as they are observed in the real world.

Fair enough. Even so, the problem with empirical confirmation is that for a system as complex as a modern economy, any given empirical outcome is susceptible to multiple theoretical explanations. To differentiate between those, we must analyze the theory qua theory.

When theorizing about economic matters, I always find it helpful to create “toy models” that isolate the problem being discussed - so let’s do that here. Please note that these are my models, developed to help me think, so an errors must be attributed to me and not Douglas or Heydorn.

Economic Model #1: Pre-Industrial Production

Assume there are two firms in the economy, X and Y, each of which is owned and operated by entrepreneurial crafter Cx and Cy respectively. Firm X produces good Gx (raw materials), which it sells to Firm Y. Gx is used by Firm Y to produce Gy (the economy’s only consumer good). Neither firm has any overhead. We will assume a debt-free exogenous money is in circulation.

Firm X pays Cx an amount of wages Wx to produce Gx. Since Cx is owner, operator, and employee, we need not differentiate between wages and profits.² The price of Gx, which we’ll call Px, is therefore simply Wx.

Firm Y, likewise, pays Cy an amount of wages Wy to produce Gy. However, Firm Y must also pay for the raw materials Gx that were used, which cost Px. The price of goods Py for Gy is therefore Wy + Px.

Has effective demand been created to purchase Gy? Yes. If Py = Wy + Px, and Px = Wx, then Py = Wy + Wx. The total price of all consumer goods in the economy equals the total wages paid out. Supply meets demand, and Say’s Law holds true!

Have we so easily disproven the A + B theorem?

No, says Douglas. In his 1936 book Approach to Reality, Douglas clarified that only “under certain circumstances, almost universal in modern industry, purchasing power cannot be equal to prices, if purchasing power and prices are both considered as a flow.”

So what would be an exception to these certain circumstances? Heydorn explains that in the old days of pre-industrial “hand production,” the Social Credit theorem would not have applied:

If we were to imagine a multi-stage process of hand production, involving no other costs but those of labor and no profit³, the total flow of consumer incomes stemming from that production could be equated to its total flow of final prices by maintaining that production in a steady-state of self-repeating motion. That is, the consumer incomes obtained from the present production of the intermediate stages of future goods would be sufficient, together with the incomes distributed by the final stage of production, to offset the prices of the final stage in each succeeding period.

What differentiates pre-industrial production from industrial production is, of course, industry — that is, real capital such as factory machines. Let’s explore that.

Economic Model #2: Industrial Production

Assume there are two firms in the economy, X and Y, each of which is owned and operated by a capitalist-laborer Cx and Cy respectively. We will again assume a debt-free exogenous money is in circulation.

Each of the firms owns a factory, which depreciates at a rate of Dx and Dy respectively each production cycle.

Firm X pays Cx an amount of wages Wx to produce Gx. However, the price Px is no longer simply Wx. Firm X must, in its costs, account for the depreciation of its factory by setting aside a reserve to pay for a new factory in the future. Therefore, Px = Wx + Dx.

Firm Y, likewise, pays Cy an amount of wages Wy to produce Gy. However, Firm Y must also pay for the raw materials Gx that were used, which cost Px. And it, too, must set aside a reserve to pay for a new factory in the future.

The price of goods Py for Gy is therefore Wy + Dy + Px. Px = Wx + Dx. So the price of goods Py = Wy + Wx + Dy + Dx. Unfortunately, a set-aside for depreciation is saved, not spent. Therefore, the effective demand created by the production cycle is only Wy + Wx. There is a shortage of demand for the goods!

Because the firms set aside a reserve for factory depreciation, the total price of all consumer goods in the economy becomes greater than the total wages paid out. Supply does not meet demand, and Say’s Law does not hold true.

This is the simplest possible demonstration of the A + B Theorem. What Douglas calls A is simply what I have called Wx + Wy. And what Douglas calls B is what I have called Dx + Dy. Total cost of consumer goods is greater than funds available to consumers (A) because of depreciation (Dx + Dy).

When presented with the A + B theorem as such, the first criticism leveled against it is “that can’t be right; the economy can’t work like that; if it did it would have collapsed long ago!” Against this criticism, Heydorn retorts:

Douglas’s claim is that no isolated productive cycle can balance prices and incomes under the specified conditions… Hence the corollary theorem that new purchasing power must be added from an extraneous source if the totality of those goods and services (both within the producer’s internal market and in the consumer’s market) is to be sold. Clearly additional purchasing power is being provided in this way; if this were not the case, our economy would have collapsed long ago.” (emphasis added)

In making this toy model, I have ignored all of the possible sources of this additional purchasing power. In fact, I have simply assumed away many factors of importance. To genuinely demonstrate the truth of the A + B Theorem, our model would have to account for factors such as:

• the introduction of purchasing power through export;

• the introduction of purchasing power through increase in money supply available to firms and consumers;

• the nominal cost of the money used by the firms and consumers;

• the nominal expenditure on building the factories by firms and the terminus to which that expenditure flows; and

• the nominal expenditure on replacing or maintaining the factories and the terminus to which that expenditure flows.

The absence of such factors creates immediate objections to the A + B theorem, and rightly so.

Who built the factories? Were did the money that was spent on building the factories go? What happens when the reserves set aside for depreciation are eventually spent either to repair the factory or to build a new factory? What happens if the economy grows? What happens if it contracts? And so on.

Critics of the Social Credit theorem argue that when taken these factors are taken into account in the context of our huge multi-stage economy, the circular flow of supply and demand is preserved in the long run, such that effective demand is actually A + B, not just A.

The creators of Social Credit theorem were not unaware of these objections, and did actually address them. However, delving into the objections and their answers is complex enough to justify a separate article, which I’ll write in the weeks ahead.

For now, I want to delve further into the implications of the theorem itself, specifically that the A < A + B problem is exacerbated by labor displacement by machinery. Heydorn explains:

One very important implication of the Social Credit theorem is that the necessary disparity in the rates of flow must be further exacerbated by the progressive displacement of labor by machinery. As technology improves, and fewer people are required to work the industrial machine, the rate at which B payments are to be made must increase relative to A payments. More money is required by firms to purchase and maintain machinery (B payments and allocated charges) and less is used to pay workers both absolutely and relatively speaking (A payments) because more machines and fewer people need to be employed. With the increase of the B factor relative to A in the generation of prices, the rate at which prices are built up must become even greater in comparison with the rate at which consumer incomes are simultaneously being distributed.

The existence of continual labor displacement means that the price system is not only not self-liquidating, but is actually ‘decreasingly self-liquidating’; i.e. the disparity in rates between price-generation and income distribution is steadily increasing…

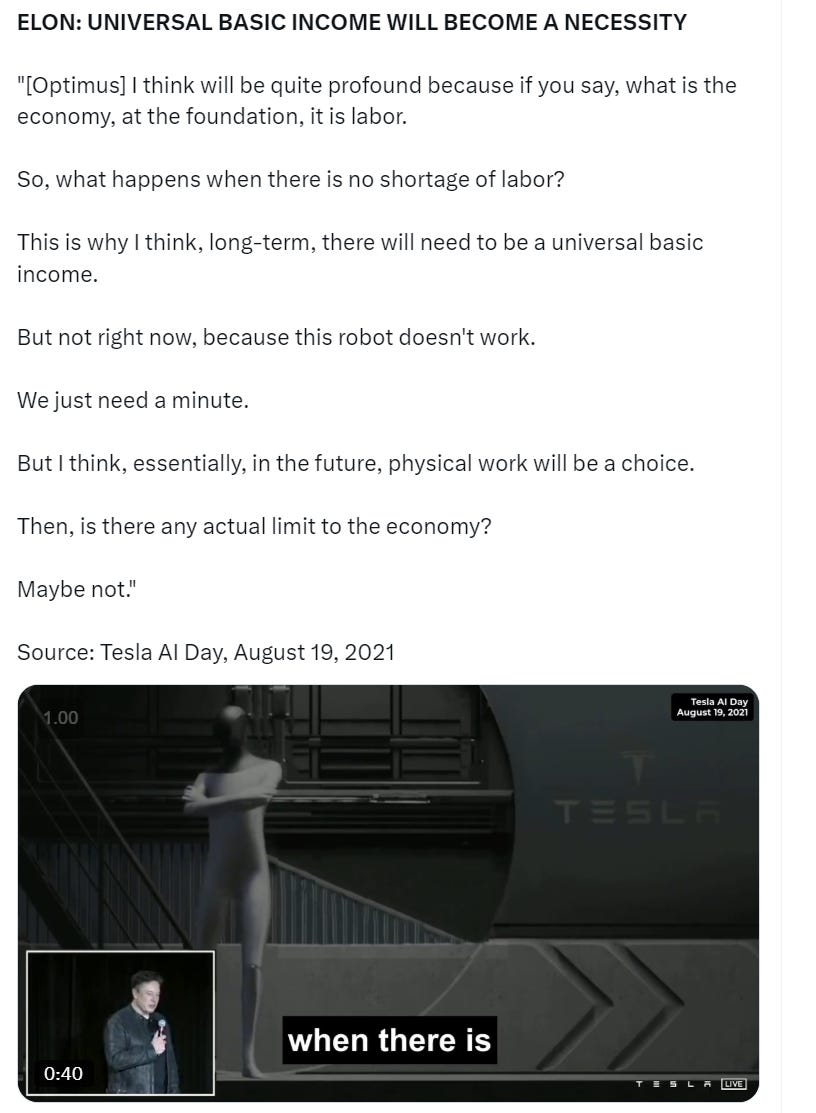
It is actually this particular implication that has led me to study Douglas Social Credit in the first place! As the reader is doubtless aware, our society is confronting the rapid introduction of artificial intelligence (AI) which, corporate managers believe, will revolutionize the economic system. Elon Musk, for instance, has argued that AI and automation will eliminate most jobs, and making a universal basic income a necessity.

We can model Elon’s proposed future using the A + B theorem. Indeed, a post-scarcity future of automated production is exactly the outcome that Douglas envisioned in the early 20th century…

Economic Model #3: Automated Production

Assume there are two firms in the economy, X and Y, each of which has an AI-controlled robotic factory. We again will assume a debt-free exogenous money is in circulation.

Each firm pays its billionaire owner a combination of salary, bonus, and dividends, which we will call Sx and Sy respectively, to manage its robotic factory.⁴

Each robotic factory slowly depreciates, again at the rate of Dx and Dy respectively each production cycle.

Firm X is a resource-and-energy supplier that supplies the material Gx that Firm Y needs to produce consumer widgets. The price that Firm X charges for Gx is Px. Px must equal Sx + Dx.

Firm Y purchases Gx for Px. It then feeds Gx into its factory, which creates consumer good widgets Gy, for which it charges Py.

The price of goods Py for Gy is therefore Sy + Dy + Px. Since Px = Sx + Dx, the price of goods Py = Sy + Sx + Dy + Dx. But the effective demand created by the production cycle is only Sy + Sx. The billionaires can afford to buy some of the consumer goods Gy, but no one else can (as there are no wage payments). They can’t buy all of the goods because money has to be set aside for depreciation.⁵

The A + B theorem thus leads to the same conclusion that Musk, Altman, et. al believe: a fully-automated future will require an injection of money to consumers or it won’t work. The exact form that Douglas Social Credit proposes is quite different from contemporary UBI theory, but that, too, will have to wait for a future article.

For now we must (as always!) close on a grim note.

The Future Already Happened Once Before

While the concept of autonomous robots who work wagelessly to provide goods and services is, at present, still science-fiction, there is an economy that dealt with a similar problem: The economy of the Roman Empire.

In the aftermath of the Roman conquests of the Mediterranean region, the Roman economy was flooded by millions and millions of slaves. Slaves were purchased for a price at a slave auction, and then worked for their owner over the course of their useful life; during that useful life they had to be housed, fed, and clothed. But this is, economically, no different than purchasing a capital good with a useful life, and paying depreciation costs against that capital good over its useful life. From a strictly economic viewpoint (e.g. ignoring the enormous human suffering involved), slaves were self-replicating robot workers.

What was the result of the introduction of enormous amounts of self-replicating robot workers as capital goods into the Roman economy? It was, of course, the impoverishment of the Roman middle and working classes. The urban proletariat of Rome survived by two means:

• The Roman Empire provided them with a dole of grain, olive oil, and other goods. In modern terms, the government gave unemployed citizens welfare payments.

• The Senatorial class provided them with goods and services in exchange for their support as “clients,” e.g. voters, flunkies, henchmen. In modern terms, politicians paid unemployed citizens to attend political rallies.

Sound familiar?

The greatest minds of the Roman Empire never managed to solve this problem, and the flourishing Roman economy eventually degenerated into the Dark Age of serfdom and feudalism. Could Douglas Social Credit theorem have saved the Roman economy? Can it save the American?

Or is it, in fact, a specious theory, nonsensical when applied at the macroeconomic level, merely an illusion created by mistakenly isolating certain aspects of production without seeing the big picture? Is there, in fact, no problem at all - or, perhaps, a different problem altogether?

Tune in next week as we contemplate such questions on the Tree of Woe.

1. I have written elsewhere that one should pay attention to whichever side in a debate is the first to lapse into ad hominem disparagement rather than continue with the next nth-order response. That side is virtually always the propagandist in the debate.

2. For an explanation of why this is the case, please see my 2020 article Solving the Profit Puzzle, which explains that in aggregate profit is the consumption expenditure of capitalists that made from the dividends and revenue share they pay to themselves.

3. Heydorn here is adopting what Professor Reisman calls “the primacy of wages,” which mistakenly views profit as something extracted from wages, in contrast to the Austrian “primacy of profits” doctrine which .

4. Again we do not need to differentiate between salary and profit. To the extent that a firm charges a higher price, it earns a higher profit, which it pays that out as dividend to its billionaire owner. Everything is always reflected in the total value Sx.

5. Even if they could buy all the goods, the rest of the population would be impoverished, but this is actually a separate consideration from the ultra-simplified version of the A + B Theorem presented here.